2023. 6. 26. 13:44ㆍComputer Science
1. 배열(Array)
가장 기본적인 자료구조이며 여러개의 변수를 담는 공간으로 이해할 수 있다.
배열은 인덱스(Index)가 존재하고 인덱스는 0부터 시작한다.
특정한 인덱스에 직접적으로 접근이 가능하고 수행시간은 O(1)을 가진다.
장점: 캐시(cache) 히트 적중률이 높고 조회가 빠르다.
단점: 배열의 크기를 미리 지정해야 하는 것이 일반적이며 데이터의 추가 및 삭제에 한계가 있다.
캐시히트 적중률이란?
CPU(클라이언트)에서 요청한 데이터가 캐시에 존재하여 이를 이행할 수 있을때 캐시 히트(Hit)라고 한다.
| Memory address | 0x0000 | 0x0004 | 0x0008 |
| Index | 0 | 1 | 2 |
| Value | 10 | 30 | 70 |
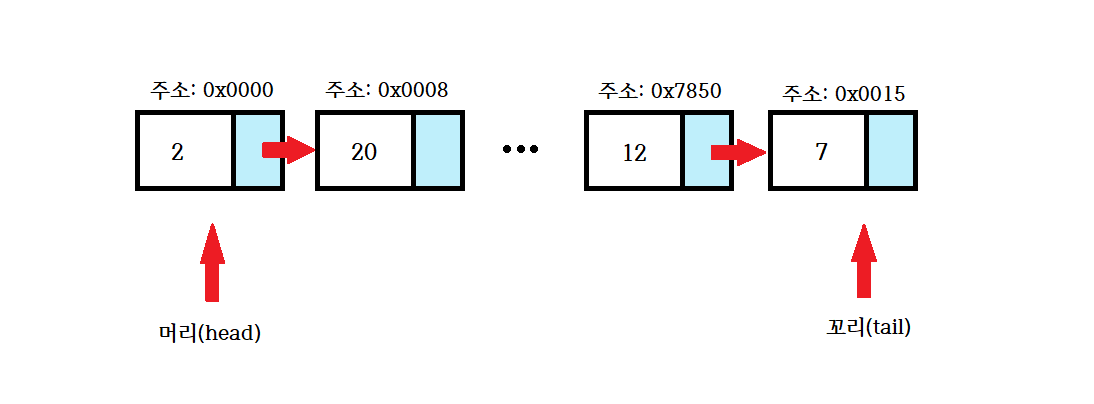
2. 연결리스트(Linked List)
연결 리스트는 메인 메모리상에서 주소가 연속적이지 않으며 배열과 다르게
크기가 정해져있지 않고 동적으로 변경이 가능한 것이 특징이다.
장점: 포인터가 다음 데이터의 위치를 가지고 있기 때문에 삽입과 삭제가 간편하다.
단점: 특정 인덱스의 원소를 검색할때 앞에서부터 원소를 찾기 때문에 검색속도가 느리다.
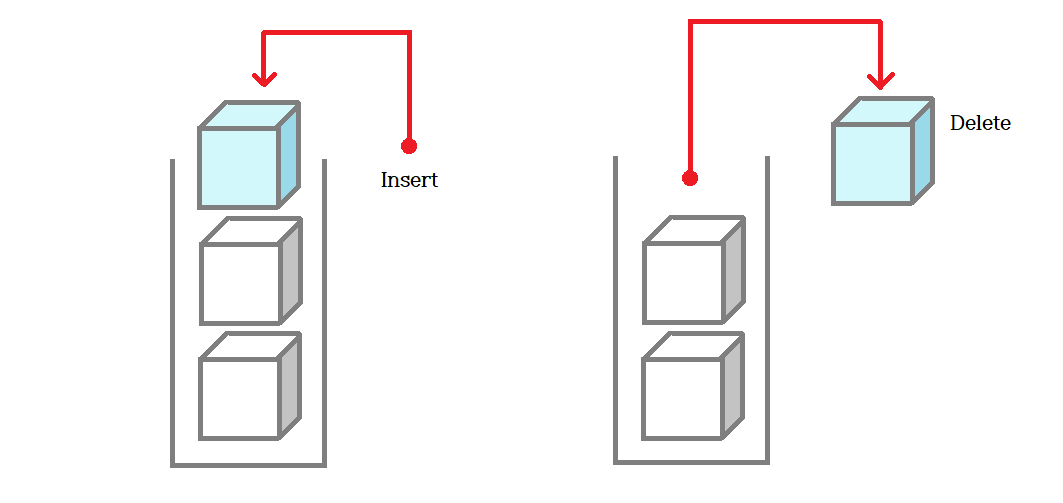
3. 스택(Stack)
먼저 들어온 데이터가 나중에 추출되는 자료구조이며 박스가 쌓인 형태를 스택이라고 볼 수 있다.
새로운 원소를 삽입할때는 마지막위치에 삽입하고 삭제할때 마찬가지로 마지막 위치에서 삭제된다.
4. 큐(Queue)
큐는 먼저 삽입된 데이터가 먼저 추출되는 자료구조이다.
예시로 게임 대기 큐의 경우 먼저 대기한 사람이 먼저 게임에 매칭되는 것과 동일하다.

Javascript Queue
Javascript에서는 큐 라이브러리를 기본적으로 제공하고있지 않기 때문에
간단하게 Queue 라이브러리를 직접 작성하여 사용할 수 있다.
필자 역시 Javascript를 주로 사용하기 때문에 Queue라이브러리를 만들어 두었다.
class Queue {
constructor() {
this.items = {};
this.headId = null;
this.tailId = null;
this.length = 0;
}
size() { return this.length; }
isEmpty() { return this.length === 0; }
enq(item) {
if (!this.headId) this.headId = 0;
if (this.headId == 0) {
this.items[this.length] = item;
this.length++;
this.tailId = this.length - 1;
}
else {
this.tailId++;
this.items[this.tailId] = item;
this.length++;
}
}
deq() {
if (this.isEmpty()) throw new Error('Queue is empty');
if (this.length == 0) return
this.length--;
const item = this.items[this.headId];
delete this.items[this.headId];
this.headId++;
if (this.length == 1) this.tailId = this.headId;
if (this.length == 0) {
this.headId = null;
this.tailId = null;
}
return item;
}
head() {
if (this.isEmpty()) throw new Error('Queue is empty');
return this.items[this.headId];
}
tail() {
if (this.isEmpty()) throw new Error('Queue is empty');
return this.items[this.tailId - 1];
}
}혹시나 블로그를 방문하시는분들께서 javasciprt Queue가 필요하셨다면 사용하셔도 무방합니다.
5. 트리(Tree)
트리는 계층적인 구조를 표현할 때 사용할 수 있는 자료구조다.
나무를 뒤집은 것 같은 형태이다.
- 루트 노드(root node): 부모가 없는 최상위 노드
- 단말 노드(leaf node): 자식이 없는 노드
서로 같은 부모를 가지는 노드간의 관계를 형제관계라고 하며 루트노드에서의 길이를
깊이(depth)라고 한다. 이는 즉 출발노드에서 목적지 노드까지 거쳐야 하는 간선의 수를 의미한다.
트리의 높이(height)는 루트 노드에서 가장 깊은 노드까지의 길이를 의미한다.
트리의 종류
- 이진 트리(Binary Tree): 최대 2개의 자식을 가질 수 있는 구조의 트리를 말한다.
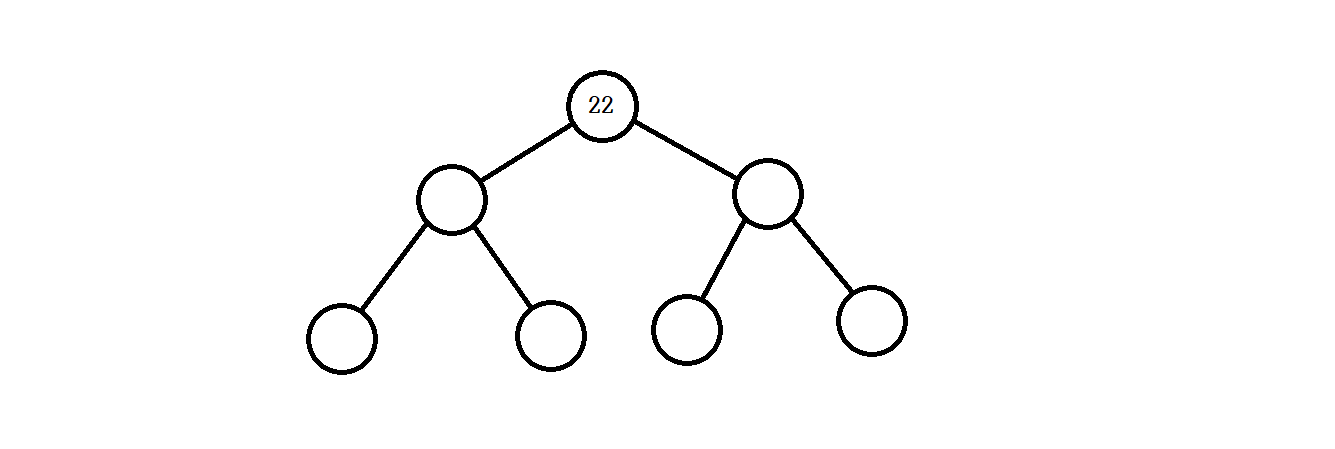
- 포화 이진 트리(Full Binary Tree): 리프노드를 제외한 모든 노드가 두 자식을 가지고 있는 트리다.
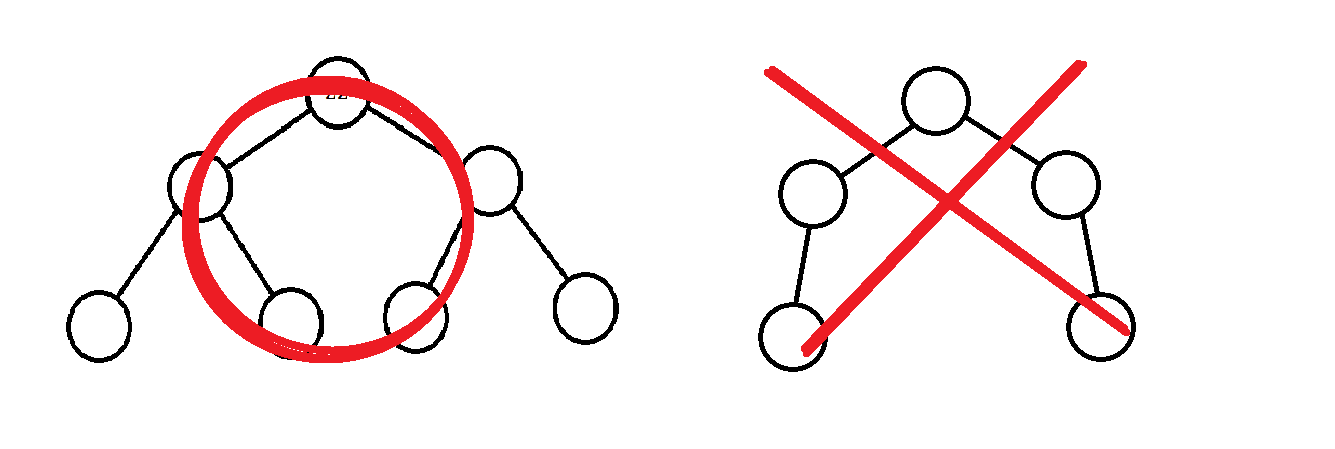
- 완전 이진 트리(Complete Binary Tree): 모든 노드가 왼쪽 자식부터 차례로 채워진 트리다.
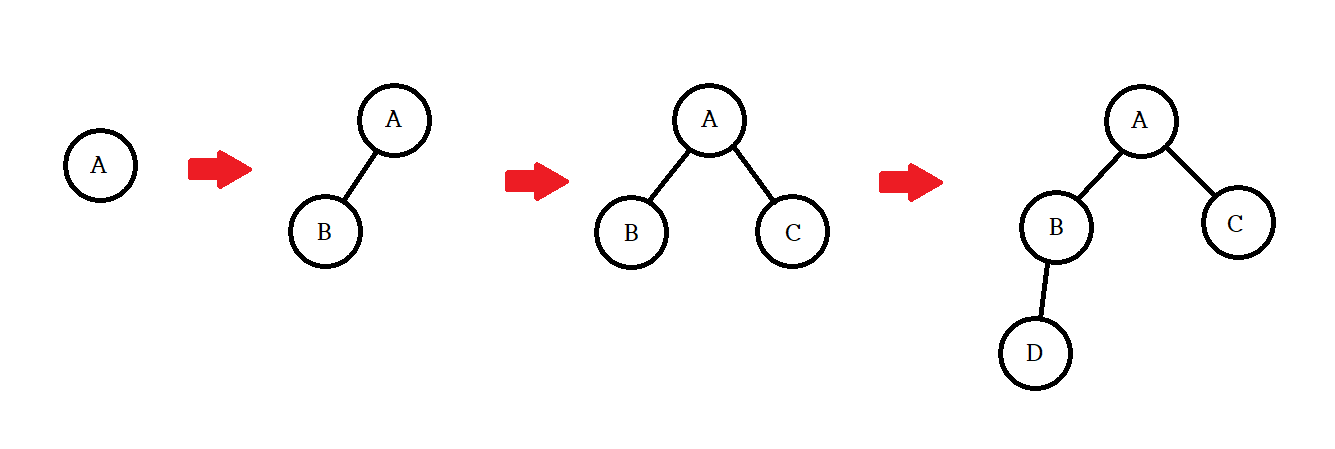
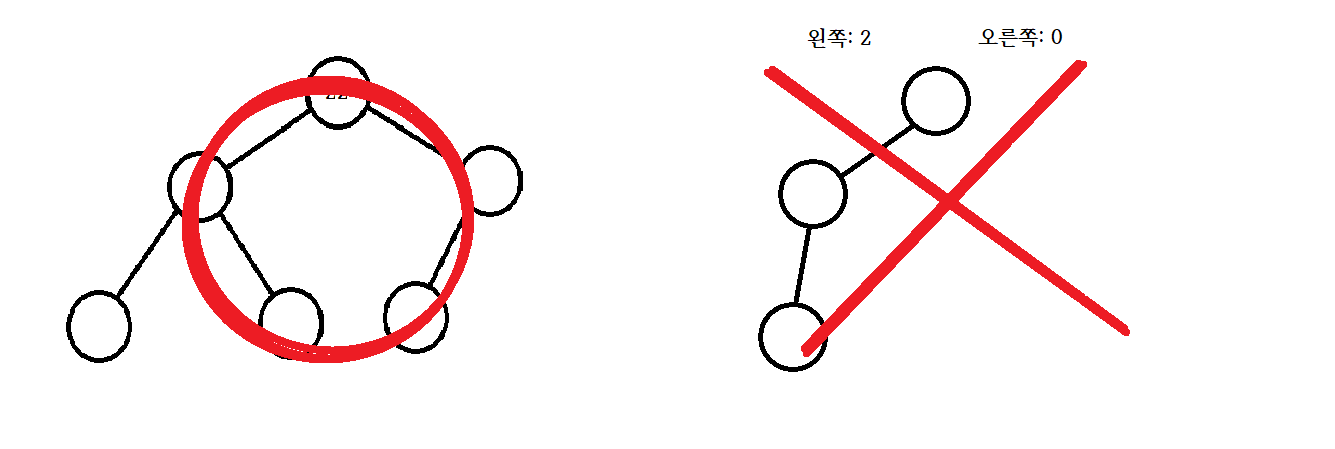
- 높이 균형 트리(Height Balanced Tree): 왼쪽과 오른쪽 자식 트리의 높이가 1이상 차이가 나지 않는 트리다.
6. 힙(Heap)
힙은 원소중 최댓값 또는 최솟값을 빠르게 찾아내는 자료구조이다.
원소 삽입과 삭제할때 O(logN)의 수행시간을 요구하며 N개의 데이터를 힙에 넣었다
모두 꺼내는 작업은 정렬과 동일하여 수행시간 O(N log N)을 요구한다.
힙은 완전 이진트리 자료구조를 따르며 우선순위가 가장 높은 노드가 루트에 위치한다.
1. 최대 힙(max heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 항상 크다.
- 루트 노드가 가장 크며, 값이 큰 데이터가 우선순위를 가진다.
2. 최소 힙(min heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 항상 작다.
- 루트 노드가 가장 작으며, 값이 작은 데이터가 우선순위를 가진다.
7. 우선순위 큐(Priority Queue)
우선순위에 따라서 데이터를 추출할 수 있는 자료구조다.
우선순위 큐는 일반적으로 힙(heap)을 이용해 구현하며 배열 자료형으로도 구현가능하다.
| 우선선순위 큐 구현방식 | 삽입 시간 | 삭제 시간 |
| 배열 자료형 | O(1) | O(N) |
| 힙(Heap) | O(logN) | O(logN) |
일반적으로 우선순위 큐는 이진트리 구조를 사용한다.
javascript는 기본적으로 우선순위 큐 라이브러리를 제공하지 않기 때문에 필요한 경우
별도의 라이브러리를 사용해야 한다.
참고할 수 있는 깃허브: https://github.com/ndb796/priorityqueuejs
8. 그래프(Graph)
그래프는 특정 노드의 정점과 노드와 노드의 간선을 나타내기 위한 자료구조이다.
그래프는 두가지 방식으로 구현할 수 있다.
- 인접행렬: 2차원 배열을 사용하는 방식
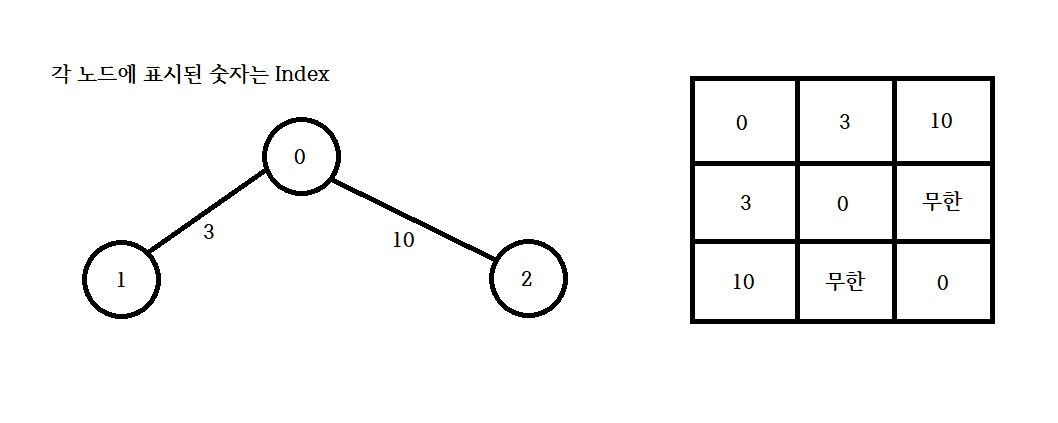
각 인덱스에 각 노드가 자리해 있으며 위 이미지의 표를 배열로 표현한다면 아래와 같다.
[0, 3, 10]
[3, 0, infinity]
[10, infinity, 0]
각 행은 각 노드의 인덱스번호부터 출발했을때 얻을 수 있는 비용이다.
즉 0, 1, 2 의 인덱스를 가지고 있기 때문에 행에 3의 길이여야 하고
각 인덱스에서 출발한다고 가정하면 1행에서 인덱스 0번자리는 자기 자신이기 때문에
비용이 발생하지 않아 0이다. 다음 인덱스 1번자리는 0번노드 -> 1번노드로 이동하는
비용이 3이다. 그리고 0번노드 -> 2번노드는 비용이 10이기 때문에 결과적으로
1번째 행은 [0. 3, 10]이 되는 것이다. 나머지 값들도 모두 동일하게 적용되며
간선이 없어 갈 수 없는 경우는 무한(infinity)으로 표기한다.
- 인접리스트: 연결 리스트를 이용하는 방식
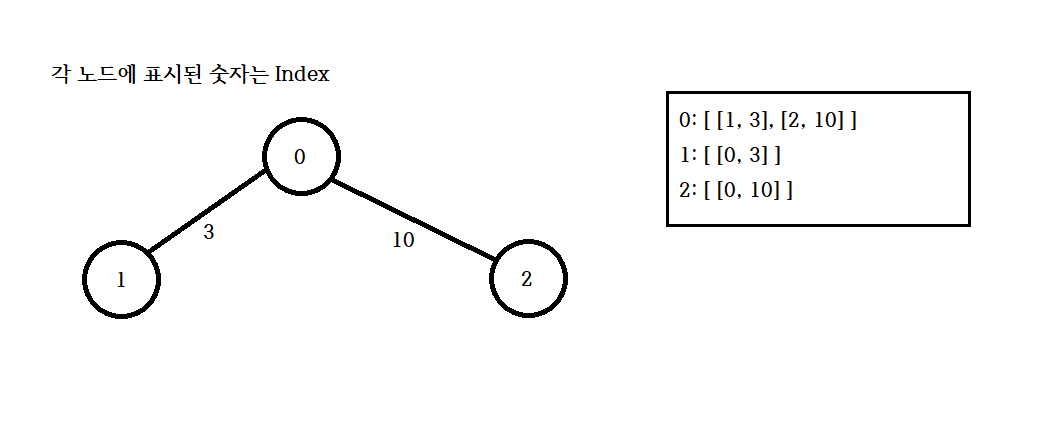
인접 리스트의 경우 노드의 각 인덱스를 각 열로 나열하고 연결가능한 노드와 간선비용을 저장한다.
0번노드의 경우 1번노드와 2번노드를 연결 할 수 있고 1번노드와 연결하면 비용은 3,
2번노드와 연결하면 비용은 10이기 때문에 최상단 행이(index 0번 노드) [1, 3], [2, 10]를 가지게 된다.
나머지도 마찬가지로 연결이 불가능한 경우는 모두 제외하고 연결이 되는 경우만
연결되는 노드번호와 간선의 비용만 저장한다.
그래프의 시간 복잡도
- 인접행렬: 모든 정점들의 연결 여부를 저장해 O(V²)의 공간을 요구한다.
공간효율성이 좋지 않지만 두 노드의 연결 여부를 O(1)의 시간만을 요구한다. - 인접리스트: 연결된 간선의 정보만을 저장하여 O(V + E)의 공간을 요구한다.
공간효율성이 좋은편이지만 두 노드의 연결여부를 확인하는데 O(V)의 시간이 요구된다.
마치며...
지난 알고리즘 학습을 복습하면서 포스팅을 진행하고 있는데 초기에 학습했던 내용들이 분명 학습당시엔 명료했던 이해도가 시간이 지나니 흐리게 남아있는 경우가 많은 것 같다. 정말 기록하는 것은 중요하고 어떠한 키워드를 가지고 생각하며 기록해야하는지를 다시한번 하게 되었다.
'Computer Science' 카테고리의 다른 글
| [ Algorithm ] 탐욕 알고리즘 (0) | 2023.06.27 |
|---|---|
| [ Algorithm ] 정렬 알고리즘 (0) | 2023.06.26 |
| [ Algorithm ] 자료구조와 Big-O 표기법 (0) | 2023.06.25 |
| [ Blocking / Non-Blocking ] 통신 처리방식 (0) | 2022.11.26 |
| [ TCP / UDP ] 특징과 차이점 (0) | 2022.11.26 |